排序

一、排序算法的种类

O（n^2）的排序方法包括选择排序、冒泡排序等。

O（nlogn）的排序方法包括归并排序、快速排序等。

C++函数sort的时间复杂度为O（nlogn），因此在编写代码时无需自己实现排序算法。学习排序算法的目的是为了理解算法的内部思想。本章仅介绍选择排序、冒泡排序、归并排序和快速排序，其他排序算法如插入排序等可在课堂上跟随老师学习。

本章节部分内容选自CSDN博客的排序算法--归并排序--详解与代码_从a定点开始各定点的归并顺序系列。

二、选择排序

选择排序（Selection sort）

选择排序是一种简单直观的排序算法。它的工作原理是每一趟从待排序的数据元素中选出最小（或最大）的一个元素，顺序放在已排好序的数列的最后，直到全部待排序的数据元素排完。

选择排序算法通过选择和交换来实现排序，其排序流程如下：

首先从原始数组中选择最小的1个数据，将其和位于第1个位置的数据交换。
接着从剩下的n-1个数据中选择次小的1个元素，将其和第2个位置的数据交换。
然后，这样不断重复，直到最后两个数据完成交换。最后，便完成了对原始数组的从小到大的排序。

示例： 定义数组 a[5]={9,10,7,8,5}；k是当前区间最小值下标

第1轮：[1,5]求最小值，因此，k=5，让a(1)和a(5)交换
第2轮：[2,5]求最小值，因此，k=3，让a(2)和a(3)交换
第3轮：[3,5]求最小值，因此，k=4，让a(3)和a(4)交换
第4轮：[4,5]求最小值，因此，k=5，让a(4)和a(5)交换

总结：第i轮：[i,n]求最小值，每轮必会得到最小值下标k=j（或者k=i自己，不用交换），让a(i)和a(k)交换，共需n-1轮加工

C++代码:

#include<iostream>
using namespace std;
#define N 10

void Select_Sort(int* arr, int n)  //arr为数据数组，n为数组长度
{
    for (int i = 0; i < n-1; i++) {
        int min = i;
        for (int j = i; j < n; j++) {
            if (arr[min] > arr[j]) {
                min = j;
            }
        }
        if (min != i) {
            swap(arr[i], arr[min]);
        }
    }
}

int main()
{
    int arr[N]= { 1,4,6,3,0,2,5,9,8,7 };
    Select_Sort(arr, 10);
    for (int i = 0; i < N; i++) {
        cout << arr[i] << ",";
    }
    cout << endl;
    return 0;
}

三、冒泡排序

冒泡排序算法的原理如下：

比较相邻的两个元素，如果前者比后者大（反之倒序），则交换。对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。针对所有的元素重复以上的步骤。持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。由于其交换过程就像泡泡往上冒，所以叫冒泡排序。

示例： 定义数组 a[5]={9,10,7,8,5}；

第1轮：
- 微观：相邻元素a(j-1)与a(j)比较，小的往前换，j在范围[2,5]内，从后往前
- 宏观：a(1)必然交换得到[1，5]内的最小值
第2轮：
- 微观：相邻元素a(j-1)与a(j)比较，小的往前换，j在范围[3,5]内，从后往前
- 宏观：a(2)必然交换得到[2，5]内的最小值
第3轮：
- 微观：相邻元素a(j-1)与a(j)比较，小的往前换，j在范围[4,5]内，从后往前
- 宏观：a(3)必然交换得到[3，5]内的最小值
第4轮：
- 微观：相邻元素a(j-1)与a(j)比较，小的往前换，j在范围[5,5]内，从后往前
- 宏观：a(4)必然交换得到[4，5]内的最小值，排序完成

共经历4次加工

总结： 第i轮：元素总数为n

微观：相邻元素a(j-1)与a(j)比较，小的往前换，j在范围[i+1, n]内，从后往前
宏观：a(i)必然交换得到[ i,n]内的最小值

供需进行n-1次加工，排序是升序

四轮排序结果图

#include<iostream>
using namespace std;
#define N 10

void Bubble_Sort(int* arr, int n)  // 参数为数组和长度
{
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n - i - 1; j++) { // n-i-1是比较次数，每比较一趟就少一次
            if (arr[j] > arr[j + 1]) {  // 交换arr[j]与arr[j+1]的值
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

int main()
{
    int arr[N] = { 1,4,6,3,0,2,5,9,8,7 };
    Bubble_Sort(arr, 10);
    for (int i = 0; i < N; i++) {
        cout << arr[i] << ",";
    }
    cout << endl;
    return 0;
}

四、快速排序

快速排序（ quicksort）是对冒泡排序的一种改进。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

设要排序的数组是A[0]…A[n-1]，首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。

举个栗子详细的说明一下：下面序列

把第一位57作为基准位，用变量把它存起来，因为一会就没了

l 把所有比57小的数放在57的左面，把比57大的数放在57的右面

l 两边同时进行，左边找大的，右边找小的，把小的放左边，大的放右边，具体操作如下：

第一趟：从指针j开始，24小于57，放到左边，把57覆盖掉

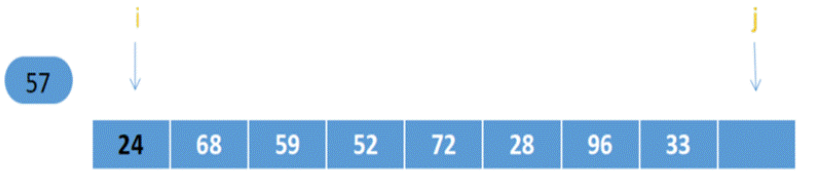
之后：指针i右移，指向68，68>57，放到右边

之后：指针j左移指向33，33<57，放到左边

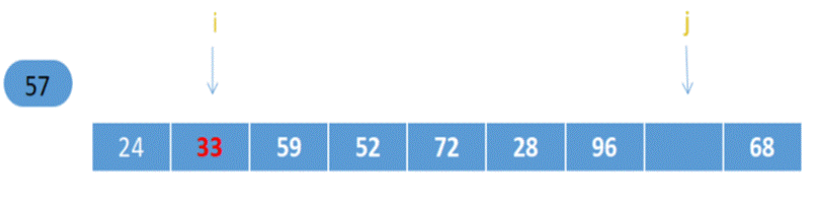
之后：指针i右移指向59，59>57，放右边

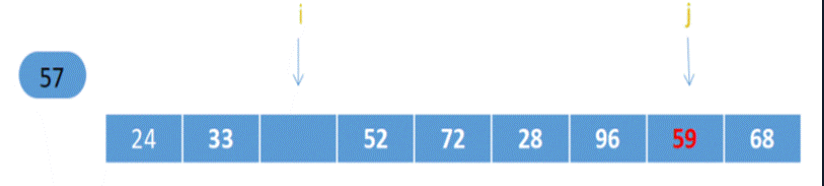
之后：指针j左移指向96，96>57，j再左移指向28，28<57，放左边

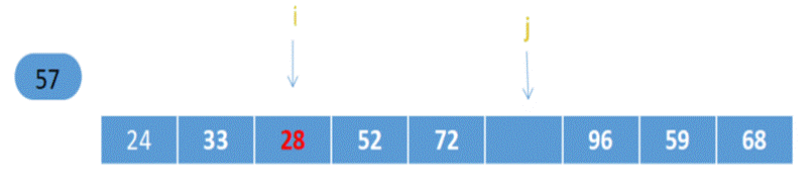
之后：指针i右移指向52，52<57,i继续右移指向72，72>57,放右边

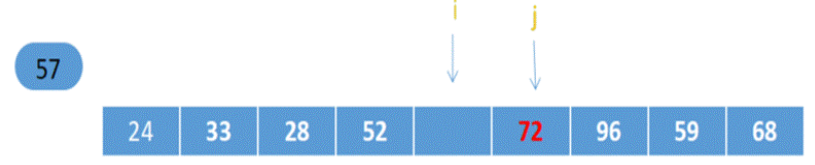
之后：指针j左移，与指针i重合指向NULL，这时放入57

这时发现左边的数都比57小，右边都比57大

然后再对57左边的数，即：0到i-1进行快速排序（同样操作，把24作为基准，左边小，右边大），对57右边的数，即：i+1到n进行快速排序（以72位基准，左边小，右边大）直到不能再进行排序为止；

// 快速排序：对冒泡排序的改进
// 思想：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，
// 然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列

#include<iostream>
#include<time.h>
using namespace std;

void randData(int* a, int n)  // 产生n个0-99的随机数，用于创建随机数组用来作为排序前数列
{
    srand(time(NULL));
    for(int i = 0; i < n; i++)
    {
        a[i] = rand() % 99;
        cout << a[i] << ",";
    }
    cout << endl;
}

void Qsort(int* a, int start, int end)  // 快速排序主体代码函数
{
    if(start >= end) return;
    int i = start;
    int j = end;
    int key = a[i];
    while (i < j)
    {
        while(i < j && a[j] >= key)
        {
            j--;
        }
        a[i] = a[j];
        while(i < j && a[i] <= key)
        {
            i++;
        }
        a[j] = a[i];
    }
    a[i] = key;
    Qsort(a, start, i - 1);
    Qsort(a, i + 1, end);
}

void show(int* a, int n)    // 输出函数
{
    for(int i = 0; i < n; i++)
    {
        cout << a[i] << ",";
    }
    cout << endl;
}

int main()
{
    const int n = 10;
    int a[n];
    randData(a, n);
    Qsort(a, 0, n - 1);
    show(a, n);
    return 0;
}

五、归并排序

归并排序：（ Merge Sort）是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（ Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并，使用中牺牲空间换取时间的算法

归并操作（merge），也叫归并算法，指的是将两个顺序序列合并成一个顺序序列的方法。

举例说明：

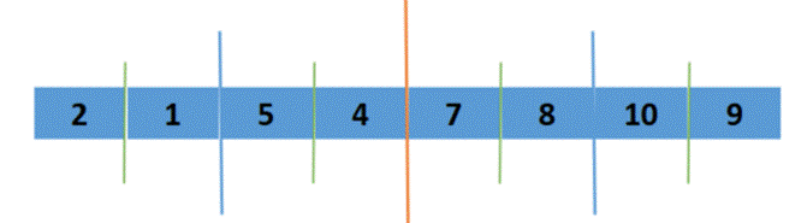
假如两个有序数列：（2，8，9，10）（4，5，6，7）合成一个大数组arr[]就是（2，8，9，10，4，5，6，7）

可以看出它的左边是有序的，右边是有序的，但是整体是无序的

我们把左边的数组，和右边的数组拆除来

我们定义几个变量分别标记记录：

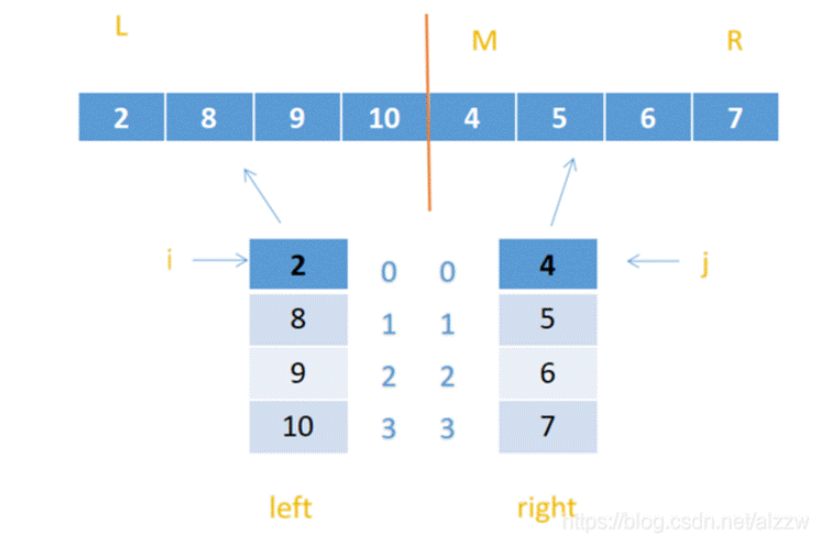
L为原始数组最左边位置，所以数组left的长度为M-L

R为原始数组最右边位置，数组right的长度为R-M+1

M为中间位置

对于原始数组arr[]：

1.首先从i与j指向的值开始比较，比较i和j指向的值哪一个小,小的赋给arr【k】即left【i】<rigth【j】，所以arr【k】 = left【i】i++，k++；

2.这时i指向8，j依然指向4，8>4，所以把4赋给arr【k】 j++，k++；

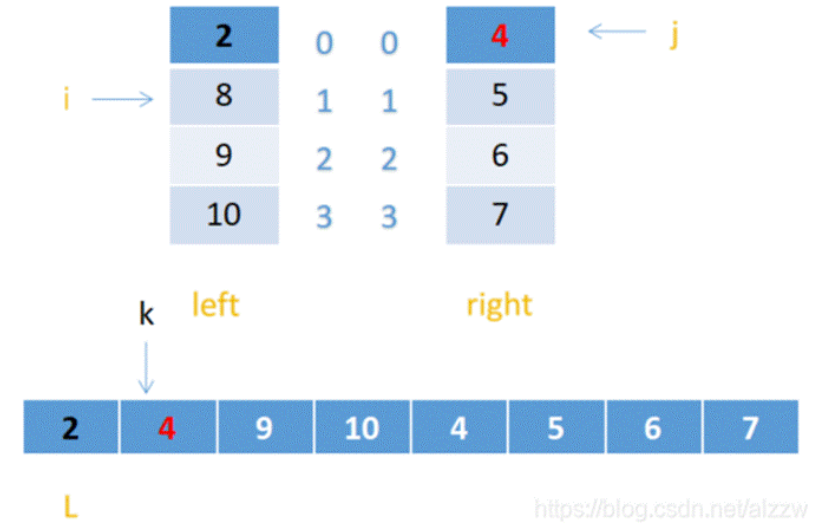
3.这时i指向8，j指向5，8>5,所以把5赋给arr【k】 J++，k++；

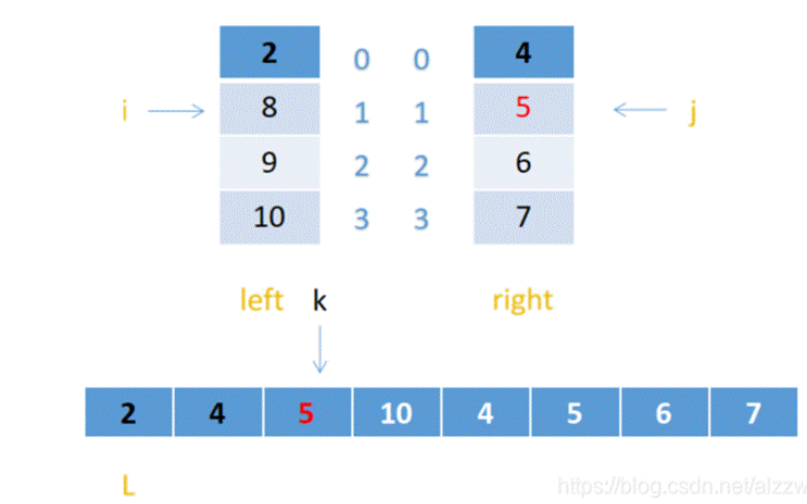
4.以此类推，当i和j不小于左右数组的长度时停止

如果：思考？

给定的数组两边不是有序的怎么办？

分治法把两边分别进行归并

假如数组为：两边都不是有序的

一分为2：左右分别归并，如果不符合要求继续一分为二，直到两边只有一个数（一个数一定是有序的）

#include<iostream>
using namespace std;

void Merge(int* arr, int L, int M, int R)  // L，M，R分别为最左，中间，最右位置
{
    int left_size = M - L;         // 左边数组大小  
    int right_size = R - M + 1;       // 右边数组大小
    int* L_arr = new int[left_size];      // 左边数组
    int* R_arr = new int[right_size];      // 右边数组

    for (int i = L; i < M; i++) {        // 给左边数组赋值
        L_arr[i - L] = arr[i];
    }
    for (int i = M; i <= R; i++) {       // 给右边数组赋值
        R_arr[i - M] = arr[i];
    }

    int i = 0, j = 0, k = L;
    while (i < left_size && j < right_size) {       // 归并
        if (L_arr[i] < R_arr[j]) {
            arr[k++] = L_arr[i++];
        } else {
            arr[k++] = R_arr[j++];
        }
    }

    while (i < left_size) {
        arr[k++] = L_arr[i++];
    }
    while (j < right_size) {
        arr[k++] = R_arr[j++];
    }
}

void Merge_Sort(int* arr, int left, int right)       // 分治
{
    if (left == right)
        return;
    else {
        int M = (left + right) / 2;
        Merge_Sort(arr, left, M);
        Merge_Sort(arr, M + 1, right);
        Merge(arr, left, M + 1, right);
    }
}

void Show(int* arr, int n)         // 输出
{
    for (int i = 0; i < n; i++)
        cout << arr[i] << ",";
    cout << endl;
}

int main()
{
    int arr[10] = { 6, 3, 2, 7, 5, 1, 4, 0, 8, 9 };
    Merge_Sort(arr, 0, 9);
    Show(arr, 10);
    return 0;
}

排序

一、排序算法的种类

二、选择排序

三、冒泡排序

四、快速排序

五、归并排序

评论