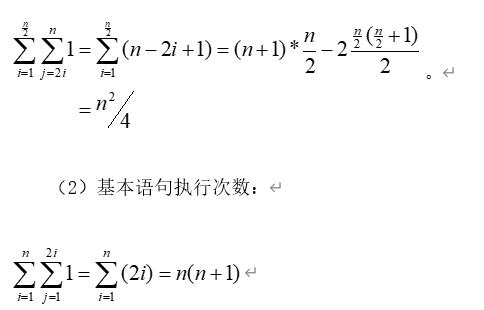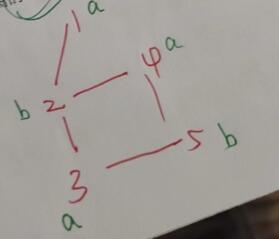算法总结

什么是算法😊？算法一般还必须满足哪些重要特性？

答：算法是对特定问题求解步骤的一种描述，是指令的有限序列。
算法还必须满足下列5个重要特性：

输入：一个算法有零个或多个输入（即算法可以没有输入）；
输出：一个算法有一个或多个输出（算法必须要有输出），通常输出与输入之间有着某种特定的关系；
有穷性：一个算法必须总是（对任何合法的输入）在执行有穷步之后结束，且每一步都在有穷时间内完成；
确定性：算法中的每一条指令必须有确切的含义，不存在二义性。并且，在任何条件下，对于相同的输入只能得到相同的输出。
可行性：算法描述的操作可以通过已经实现的基本操作执行有限次来实现。

考虑下面的算法，回答下列问题，算法完成什么功能？算法的基本语句是什么？基本语句执行了多少次？算法的时间复杂性是多少？

（1）考虑下面的算法，回答下列问题，算法完成什么功能？算法的基本语句是什么？基本语句执行了多少次？算法的时间复杂性是多少？

（1）int Mistery(int n)                    （2）int Q(int n)
{                                          {
  int  S = 0;                                 if(n = = 1)
    for(int i = 1;i < = n;i++)                   return 1;
       S = S+i*i;                             else
       return S;                                return Q(n-1)+2*n-1;            
    }                                        }

答：😜
(1)算法的基本语句是 S = S+i*i；基本语句执行了n次，算法的时间复杂性是O(n)。
(2)算法的时间复杂性是O(n)。

下面程序段中基本语句的执行次数是多少，要求写出计算公式

（1）for (i=1;i<=n;i++)        (2) m=0;
        if(2*i<=n)                 for(i=1;i<=n;i++)
        for(j=2*i;j<=n;j++)           for(j=1;j<=2*i;j++)
                y=y+i*j;                 m=m+1;

答：(1)基本语句执行次数：(n^2)/4
(2)基本语句执行次数：n(n+1)

过桥问题

有4个人打算过桥，这个桥每次最多只能有两个人同时通过。他们都在桥的某一端，并且是在晚上，过桥需要一只手电筒，而他们只有一只手电筒。这就意味着两个人过桥后必须有一人将手电筒带回来。每个人走路的速度是不同的：甲过桥要用1分钟，乙过桥要用2分钟，丙过桥要用5分钟，丁过桥要用10分钟，显然，两个人走路的速度等于其中较慢那个人的速度，问他们全部过桥最少要用多长时间？写出具体过桥的思路。

解析：
这个问题可以使用贪心算法来解决。以下是一个具体的过桥思路：

1. 假设四个人分别为甲、乙、丙、丁，他们的过桥时间分别为1分钟、2分钟、5分钟、10分钟。
2. 首先，甲和乙一起过桥，花费时间为2分钟，然后甲返回，花费时间为1分钟。
3. 接下来，丙和丁一起过桥，花费时间为10分钟，然后乙返回，花费时间为2分钟。
4. 最后，甲和乙将手电筒一起带过桥，花费时间为2分钟。

总共花费的时间为2 + 1 + 10 + 2 + 2 = 17分钟。

因此，他们全部过桥最少需要17分钟。

这种思路的关键是:通过两次最快的人一起过桥，并让最快的人回来带手电筒，以此来最大程度地减少总过桥时间。

应用选择排序方法对一个记录序列进行升序排列的基本思想是什么，具体排序过程怎么做的？

答：基本思想：第i 趟排序在无序序列ri-rn中找到值最小的记录，并和第i个记录交换作为有序序列的第一个记录。
具体排序过程如下：
（1）将整个记录序列划分为有序区和无序区，初始时有序区为空，无序区含有待排序的所有记录
（2）在无序区查找值最小的记录，将它与无序区的第一个记录交换，使得有序区扩展一个记录，同时无序区减少一个记录。
不断重复步骤（2），直到无序区只剩下一个记录为止。

#include <iostream>
using namespace std;
void selectionSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
        int minIndex = i;  // 当前最小元素的下标
        for (int j = i + 1; j < n; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j;  // 更新最小元素的下标
            }
        }
        // 交换最小元素和当前元素的位置
        swap(arr[i], arr[minIndex]);
    }
}

int main() {
    int arr[] = {64, 25, 12, 22, 11};
    int n = sizeof(arr) / sizeof(arr[0]);
    selectionSort(arr, n);
    cout << "排序后的数组：";
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
    cout << endl;
    return 0;
}

快速排序的分治策略，当以第一个记录作为轴值，对待排序序列进行划分的过程是怎样实现的？

快速排序的分治策略是：
（1）划分：选定一个记录作为轴值，以轴值为基准将整个序列划分为两个子序列r1 … ri-1和ri+1 … rn，前一个子序列中记录的值均小于或等于轴值，后一个子序列中记录的值均大于或等于轴值；
（2）求解子问题：分别对划分后的每一个子序列递归处理；
（3）合并：由于对子序列r1 … ri-1和ri+1 … rn的排序是就地进行的，所以合并不需要执行任何操作。
以第一个记录作为轴值，对待排序序列进行划分的过程为：
    （1）初始化：取第一个记录作为基准，设置两个参数i，j分别用来指示将要与基准记录进行比较的左侧记录位置和右侧记录位置，也就是本次划分的区间；
    （2）右侧扫描过程：将基准记录与j指向的记录进行比较，如果j指向记录的关键码大，则j前移一个记录位置。重复右侧扫描过程，直到右侧的记录小（即反序），若i＜j，则将基准记录与j指向的记录进行交换；
    （3）左侧扫描过程：将基准记录与i指向的记录进行比较，如果i指向记录的关键码小，则i后移一个记录位置。重复左侧扫描过程，直到左侧的记录大（即反序），若i＜j，则将基准记录与i指向的记录交换；
    （4）重复（2）（3）步，直到i与j指向同一位置，即基准记录最终的位置。

汉诺塔问题

记结论

已知刚开始时A塔座有6个碟子，这些碟子按照从上到下不断变大的次序依次放置在A塔座，即最大的碟子放在最下面，最小的碟子放在最上面，现在借助中间塔座B，将这些碟子移动到目标塔座C，要求一次只能移动一个碟子，且每次不能将大的碟子放在小的碟子上，请问要移动多少次，如果碟子数是10，移动次数是多少？如果碟子数是64，移动次数是多少？请试着写出移动次数与碟子数的函数关系或递推关系式。

正确答案：
1、碟子数为6时，移动次数63
2、碟子数为10，移动次数1023
3、碟子数是64，移动次数是2的64次方减1
4、碟子数是n，移动次数用M(n)，则所以`M(n)=2^n-1`，可以验证n=1也满足该函数关系。

试述分治法的基本思想

正确答案：
分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题，这些子问题互相独立且与原问题相同。递归地解这些子问题，然后将各个子问题的解合并得到原问题的解。

蛮力法的优缺点是什么？

正确答案：
优点：具有广泛的适用性和简单性。
缺点：计算效率不高。
应用：选择排序，顺序查找，穷举查找也是解决组合问题的一种蛮力方法。

最大子段和问题的简单算法是什么？

#include<iostream>
using namespace std;
int MaxSubsequenceSum(int arr[], int n){
    int tempSum, maxSum=0;
    for (int i = 0;i < n;i++)       // 子序列起始位置
    {
        for (int j = i;j < n;j++)   // 子序列终止位置
        {
            tempSum = 0;    
            for (int k = i;k <= j;k++)   // 子序列遍历求和
                tempSum += arr[k];
            if (tempSum > maxSum)       // 更新最大和值
                maxSum = tempSum;
        }
    }
    return maxSum;
}

int main()
{
    int a[] = { 4, -3, 5, -2, -1, 2, 6, -2 };
    int maxSubSum = MaxSubsequenceSum(a, 8);
    cout << "T结果是: " << maxSubSum << endl;
    return 0;
}

试述回溯法的基本思想及用回溯法解题的步骤。

正确答案：
答：回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。算法搜索至解空间树的任意一点时，先判断该结点是否包含问题的解。如果肯定不包含，则跳过对该结点为根的子树的搜索，逐层向其祖先结点回溯；否则，进入该子树，继续按深度优先策略搜索。  
   基本步骤:
① 针对所给问题，定义问题的解空间； 
② 确定易于搜索的解空间结构； 
③ 以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。

回溯法中常见哪两类典型的解空间树？分析各自的使用场合及时间复杂度。

正确答案：
答：回溯法中常见的两类典型的解空间树是子集树和排列树。
当所给的问题是从n个元素的集合S中找出满足某种性质的子集时，相应的解空间树称为子集树。这类子集树通常有2n个叶结点，遍历子集树需O(2n)计算时间 。
当所给的问题是确定n个元素满足某种性质的排列时，相应的解空间树称为排列树。这类排列树通常有n!个叶结点。遍历排列树需要O(n!)计算时间。

设计动态规划算法的4个步骤是什么？

正确答案：
动态规划算法的4个步骤是
（1） 找出最优解的性质，并刻画其结构特征。
（2） 递归的定义最优值。
（3） 以自底向上的方式计算出最优值。
（4） 根据计算最优值得到的信息，构造最优解。

比较分支限界法与回溯法的异同.😃

正确答案：
答：分支限界法与回溯法的相同点是：都是一种在问题的解空间树中搜索问题解的算法。
不同点：
（1）求解目标不同；
（2）搜索方式不同；
（3）对扩展结点的扩展方式不同；
（4）存储空间的要求不同。

常见的两种分支限界法的算法框架是什么?

正确答案：
答：（1）队列式(FIFO)分支限界法：按照队列先进先出（FIFO）原则选取下一个节点为扩展节点。
（2）优先队列式分支限界法：按照优先队列中规定的优先级选取优先级最高的节点成为当前扩展节点。

选择题

用3种颜色为一个具有5个顶点的无向图着色，共有（）种可能的着色组合

A、244
B、243
C、246
D、245
正确答案：B

每个点都有三种情况，所以是3^5=243

一个五个顶点的无向联通图邻接矩阵如下：

     0     1    1      0      0
     1     0    1      1      1 
     1     1    0      0      1
     0     1    0      0      1
     0     1    1      1      0

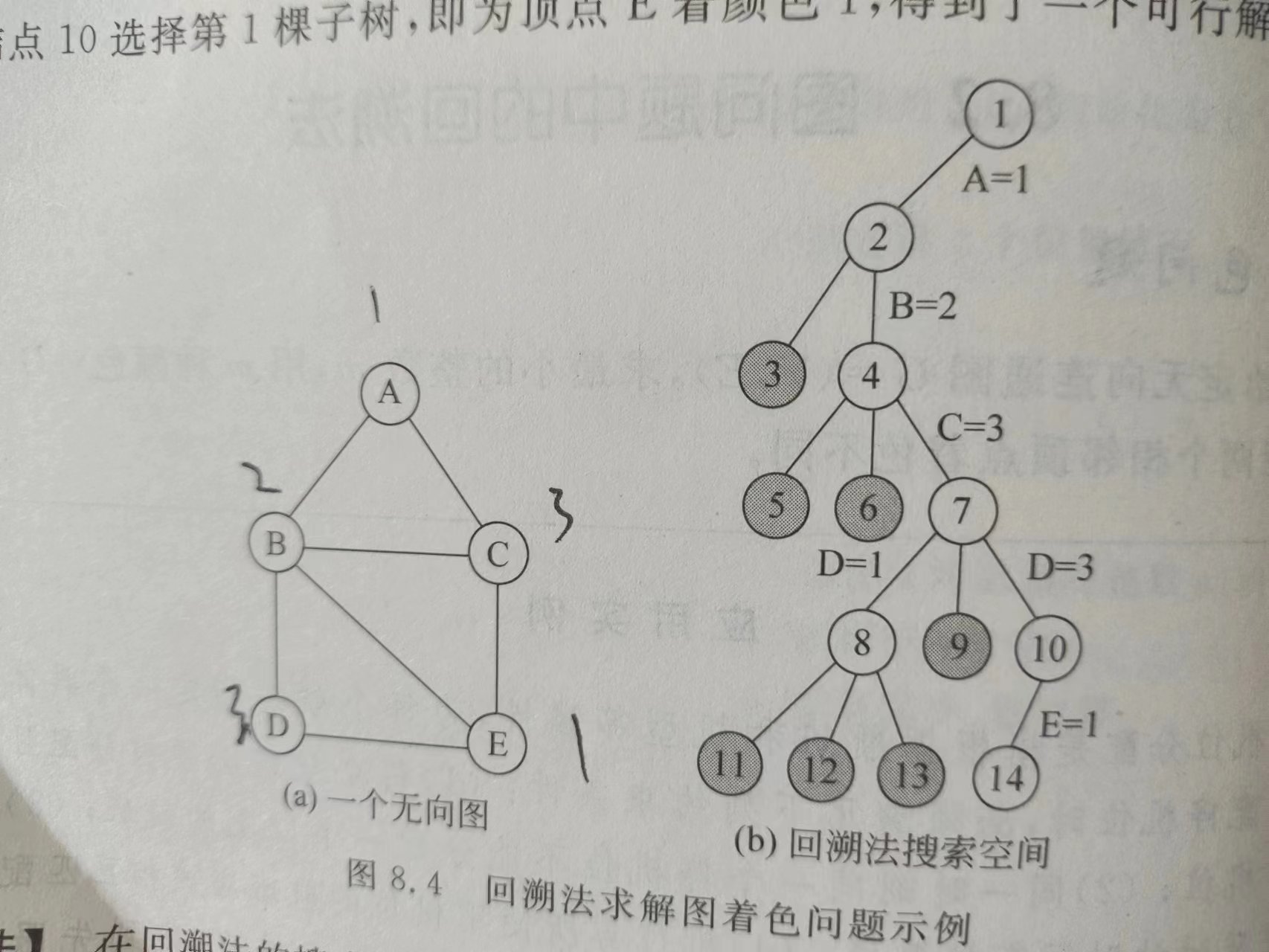
假设用3种颜色来着色，则解空间树一个完全3叉树，问：解空间树中共有（）个结点；如果用回溯法进行搜索，只需搜索其中（）个结点就找到问题的解。
A、365；14
B、363；15
C、364；14
D、365；15
正确答案：C

完全三叉树是一种特殊的三叉树结构，其中除了最后一层外，其他层的节点都被填满，且最后一层的节点从左到右连续地填入。

对于带有五个顶点无向图，其邻接矩阵如下🤣

 0     1     0     1      0 
 1     0     1     0      1
 0     1     0     1      1
 1     0     1     0      1
 0     1     1     1      0

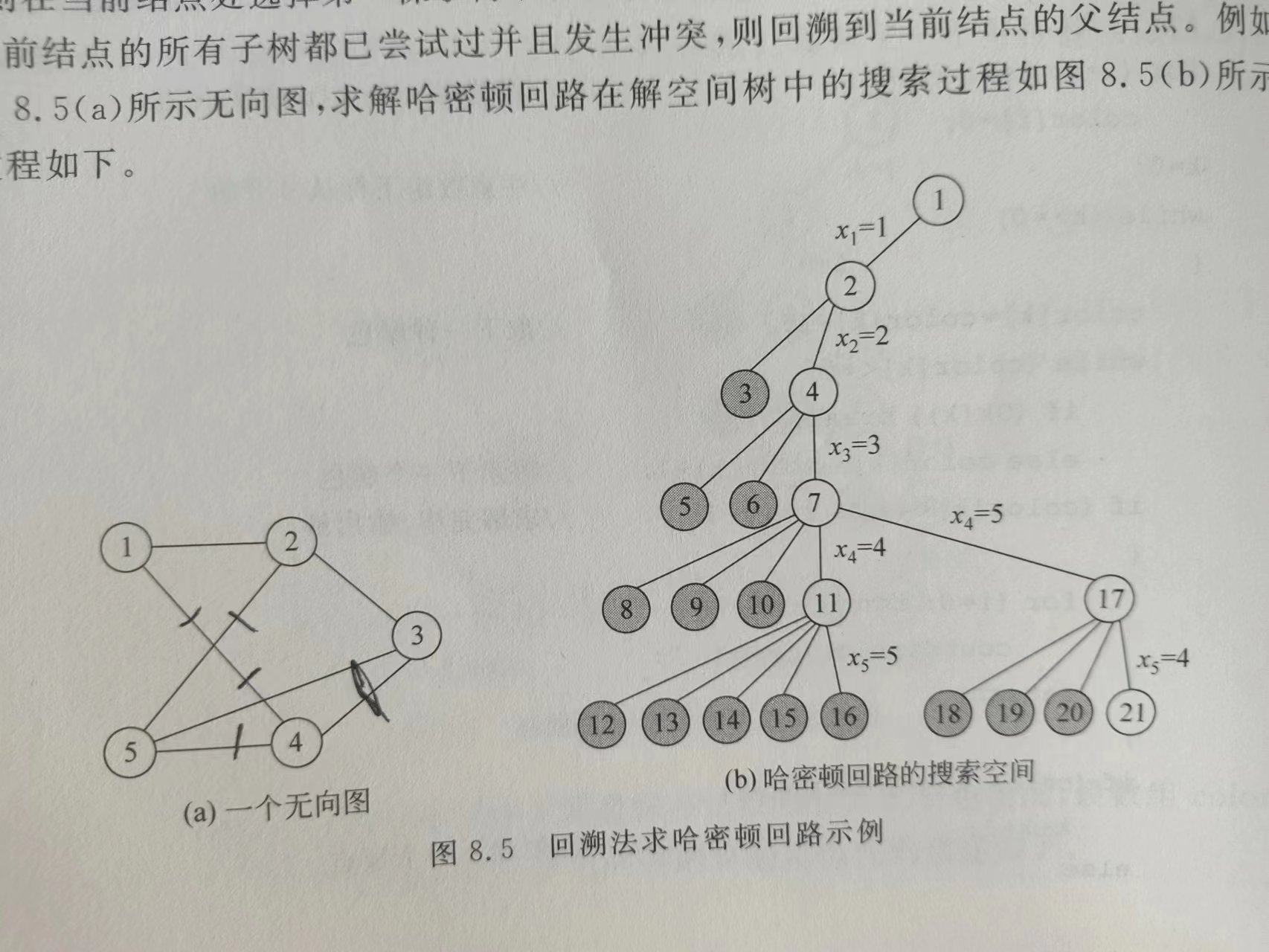
考虑该无向图的哈密顿回路问题，问：解空间树中共有（）个结点；而如果采用回溯法只用搜索其中（）个结点后就能找到问题的一个解。
A、3905；21
B、3906；24
C、3905；24
D、3906；21
正确答案：D

走楼梯问题，假设只能一次走一级台阶或走两级台阶（连续的），例如只有一级台阶，则只有一种走法；如果有两级台阶（连续的），有两种走法；如果有三级台阶，则有3种走法，问7级连续台阶共有（）走法。

A、18
B、21
C、23
D、22
正确答案：B

活动安排问题：如下六个活动集合的最大相容活动有（）个。（贪心策略选择结束时间早的活动先安排）

活动1：start=0,finish=6,start, finish表示活动的起始时刻和结束时刻，下同
活动2：start=1,finish=2；
活动3：start=3,finish=4；
活动4：start=5,finish=7；
活动5：start=5,finish=9；
活动6：start=8,finish=9；
A、5 B、4 C、3 D、6
正确答案：B

这种贪心算法的核心思想是选择结束时间最早的活动，并且确保每次选择的活动与已选择的活动不发生时间冲突，以获得最大相容活动的子集。

背包问题（注：这里是分数背包，不是0/1背包）：有三个物品，其重量和价值如下所示：

            重量                价值
物品1        20                  60
物品2        10                  50
物品3        30                  120

背包的容量为50，下面考虑三种贪心策略（1）选择物品按照价值从大到小的次序；（2）选择物品按照重量从小到大的次序；
（3）选择物品按照单位重量价值从大到小的次序。则这三种策略（1）、（2）、（3）装入背包的物品价值分别是多少（）
A、180、195、200 ；B、180、190、200；
C、185、190、195；D、185、195、200
正确答案：B

用贪心算法求解问题应该满足（）两个性质

A、最优子结构、重叠子问题；B、最优子结构、贪心选择
C、贪心选择、局部最优；D、以上都不是
正确答案：B

图着色问题：已知五个顶点无向连通图的邻接矩阵如下：

   0        1       0        0         0
   1        0       1        1         0
   0        1       0        0         1
   0        1       0        0         1  
   0        0       1        1         0

当任意两个相邻的顶点着色都不同时，该无向图的最小着色数是（）。
A、3；B、4；C、2；D、1
正确答案：C

二叉查找树

已知二叉查找树中查找概率分别是0.1、0.2、0.4、0.3，已知应用动态规划算法求最优二叉查找树的动态规划函数为C[i][i-1]=0，i=1，2，…n+1，C[i][i]
=pi，i=1，2，…，n ，C[i][j]=min{C[i][k-1]+C[k+1][j]
+（查找第i个记录一直到第j个记录概率之和）}，这里（1≤i≤j≤n，i≤k≤j）
C[2][4]的值是多少?
A、1.5；B、1.4；C、1.6；D、1.3
正确答案：B

下列算法中通常以自底向上的方式求解最优解的是

A、备忘录法；B、动态规划法
C、贪心法；D、回溯法
正确答案：B

下面问题（）不能使用贪心法解决。

A、单源最短路径问题；B、 N皇后问题
C、最小生成树问题； D、背包问题
正确答案：B

回溯法搜索状态空间树是按照（）的顺序。

A、中序遍历
B、广度优先遍历
C、深度优先遍历
D、层次优先遍历
正确答案：C

下面哪种函数是回溯法中为避免无效搜索采取的策略（）

A、递归函数
B、剪枝函数
C、随机数函数
D、搜索函数
正确答案：B

常见的两种分支限界法为（）

A、广度优先分支限界法与深度优先分支限界法
B、队列式（FIFO）分支限界法与堆栈式分支限界法
C、排列树法与子集树法
D、队列式（FIFO）分支限界法与优先队列式分支限界法
正确答案:D

采用最大效益优先搜索方式的算法是（）。

A、分支界限法
B、动态规划法
C、贪心法
D、回溯法
正确答案：A

一个C程序的执行是从（）。

A、本程序的main函数开始，到main函数结束
B、本程序文件的第一个函数开始，到本程序文件的最后一个函数结束
C、本程序的main函数开始，到本程序文件的最后一个函数结束
D、本程序文件的第一个函数开始，到本程序main函数结束
正确答案：A

在 C 语言中，每个语句必须以（）结束。

A、回车符 B、冒号
C、逗号 D、分号
正确答案：D

二分搜索算法是利用（）实现的算法。

A、分治策略 B、动态规划法
C、贪心法 D、回溯法
正确答案：A

实现棋盘覆盖算法利用的算法是（）。

A、分治法 B、动态规划法
C、贪心法 D、回溯法
正确答案：A

哈夫曼编码的贪心算法所需的计算时间为（）

A、O(n2n) B、O(nlogn)
C、O(2n) D、O(n)
正确答案：B

下列算法中不能解决0/1背包问题的是（）

A、贪心法
B、动态规划
C、回溯法
D、分支限界法
正确答案：A

下面是贪心算法的基本要素的是（）。

A、重叠子问题
B、构造最优解
C、贪心选择性质
D、定义最优解

正确答案：C

背包问题的贪心算法所需的计算时间为

A、O(n2n)
B、O(nlogn)
C、O(2n)
D、O(n)
正确答案：B

下列算法中通常以深度优先方式系统搜索问题解的是（）。

A、备忘录法B、动态规划法C、贪心法D、回溯法
正确答案：D

回溯法的效率不依赖于下列哪些因素（）

A、满足显约束的值的个数
B、计算约束函数的时间
C、计算限界函数的时间
D、确定解空间的时间
正确答案：D

在 C 语言中，字符型数据在计算机内存中，以字符的（）形式存储。

A、原码
B、反码
C、ASCII 码
D、BCD码
正确答案：C

动态规划算法的基本要素为（）

A、最优子结构性质与贪心选择性质
B、重叠子问题性质与贪心选择性质
C、最优子结构性质与重叠子问题性质
D、预排序与递归调用
正确答案：C

论述题

旅行者问题

一个旅行者要驾车从A地到B地，A、B两地间距离为s。A、B两地之间有n个加油站，已知第i个加油站离起点A的距离为di公里,输入的di从小到大，s车加
满油后可行驶m公里，出发之前汽车油箱为空。应如何加油使得从A地到B地沿途加油次数最少？给出用贪心法求解该最优化问题的贪心选择策略
，写出该最优化问题的最优值和最优解的贪心算法，并分析算法的时间复杂性。

正确答案：
答：贪心选择策略：从起点的加油站起每次加满油后不加油行驶尽可能远，直至油箱中的油耗尽前所能到达的最远的油站为止，在该油站再加满油。
最坏情况下的时间复杂性：Θ(n)

证明活动安排问题的贪心算法具有整体最优解。

正确答案：

假设在某一步选择了结束时间最早的活动A作为下一个安排的活动，并且存在一个最优解中的另一个活动B，B的结束时间比A更早。我们需要证明将B替换为A并不会影响后续的活动安排。

由于B的结束时间更早，我们可以将B的活动时间段分成两个部分，一个与A不重叠的部分和一个与A重叠的部分。如果我们选择了B而不选择A，那么与A不重叠的部分仍然可以安排其他活动，而与A重叠的部分可以被A所取代。因此，将B替换为A并不会影响后续的活动安排，贪心策略仍然是最优的。

简化版：有xyh提供

算法的贪心策略是选择结束时间最早的活动，即活动1，然后将问题简化为对剩余活动中与活动1相容的活动进行活动安排的子问题。证明过程采用反证法，假设存在一个最优解不包含活动1，然后构造一个包含活动1的最优解，从而证明包含活动1的最优解是整体最优解。

举反例证明0/1背包问题

若使用的算法是按照pi/wi的非递减次序考虑选择的物品，即只要正在被考虑的物品装得进就装入背包，则此方法不一定能得到最优解（此题说明0/
1背包问题与背包问题的不同）。

正确答案：
证明：举例如：p={7,4,4},w={3,2,2},c=4时，由于7除以3最大，若按题目要求的方法，只能取第一个，收益是7。而此实例的最大的收益应该是8，取第2
,3 个。